Ulysses HISCALE Data Analysis Handbook
Appendix 10. Effect of Backscattered Electrons on the Geometric Factors of the LEMS30 Telescope (Hong MS Thesis)
When a beam of electrons collides with a solid target not all electrons would be returned to the surface. Part of them would be absorbed by the solid, part of them would be transmitted, and only the remaining are backscattered and return to the surface. Backscattering coefficient is defined as the ratio of the number of electrons which are backscattered and return to the surface to the number of the incident electrons.
Most people derive backscattering coefficients as two independent parts. One is backscattering coefficients for normal incidence h0 and the other is the incident angle a dependent part. The h0used here is proposed by Love and Scott (J. Phys. D: Appl. Phys., 11, 1369, 1978), which is:
![]()
where F1 = (-272.5 + 168.6Z - 1.925Z + 0.00822Z) x 10-4, F2(Z) = 0.2043 - 0.6543Z-0.3, E0 is the energy (in keV) of the incident electrons, and Z is the atomic number of the target material (aluminum is assumed for the telescope chamber).
Radzimski gives the backscattering coefficients as a function of an incidence angle a, incidence energy E0 and atomic number of the target material Z (see Figure A10-10):
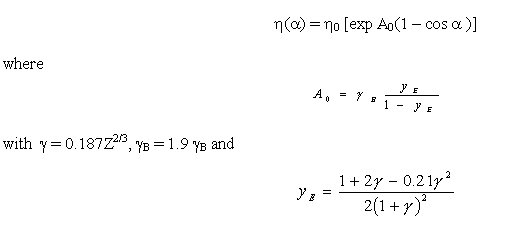
Figure A10-10 Backscattering coefficient vs. energy, Radzimski's model
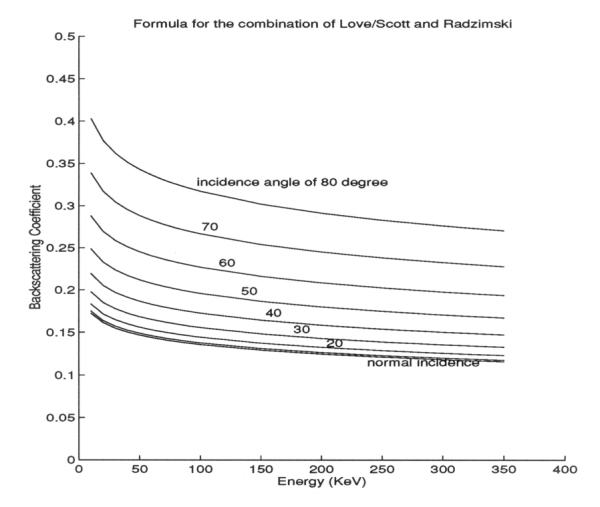
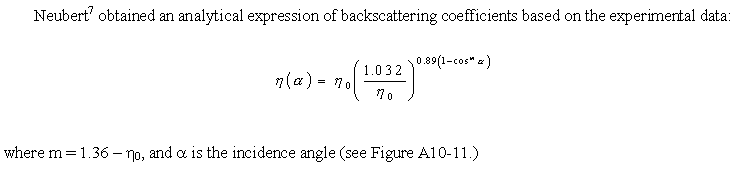
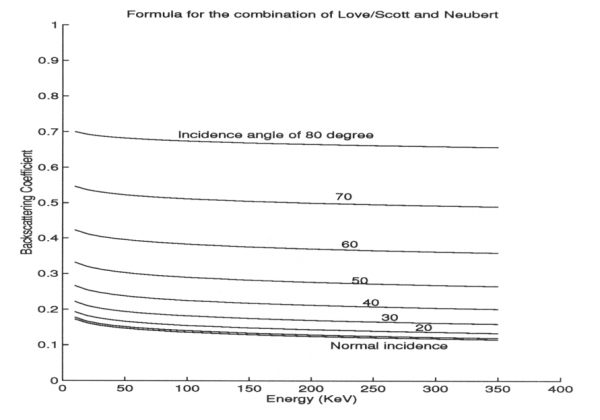
Figure A10-11 Backscattering coefficient vs. energy, Neubert's model
Next: A10.6 Appendix - Geometric Factor Approximation
Return to the Table of Contents for Hong's MS Thesis
Return to HISCALE List of Appendices
Return to Ulysses HISCALE Data Analysis Handbook Table of Contents
Updated 8/8/19, Cameron Crane
QUICK FACTS
Mission End Date: June 30, 2009
Destination: The inner heliosphere of the sun away from the ecliptic plane
Orbit: Elliptical orbit transversing the polar regions of the sun outside of the ecliptic plane



