From the results of geometric factors vs energies one can average the geometric factor for any particular energy passband:

 

 

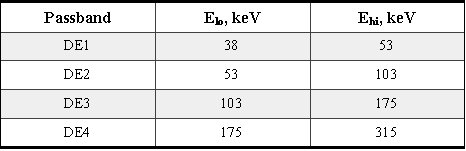
here are four energy passbands named DE channels for the B detector in the LEMS 30 telescope. The range of energies which is between Elo and Ehi for each channel is listed below:

 

Table A10-1 HISCALE deflected electron detector energy thresholds

 

 

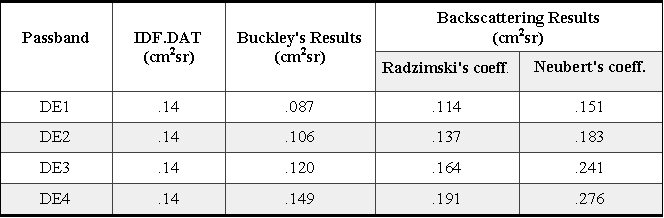
The geometric factors for different energy passbands and different backscattering coefficients are calculated and listed with the results of non-scattering (Buckley's results) and nominal values adapted for HISCALE data analysis (IDF.DAT).

 

From the results shown below one can see that backscattering electrons have significant impacts on the geometric factor of the DE channels. Notice that the Buckley results shown here are not his original results because he omitted a projected area factor of DAi for each trajectory that we have included here. See Section A10-6 for details about the calculation of an effective area. For each energy passband the geometric factor is increased by at least 30%. For the DE1 passband when Neubert's coefficients are used G is close to the IDF.DAT value. When Radzimski's coefficients are used the geometric factors for the DE1 and DE2 channels also increase nicely to get closer to the nominal values. The geometric factors of other energy passbands increase significantly and have much higher values than those of IDF.DAT. When one looks into these results one needs also to take the following into consideration.

 

Table A10-2 DE detector channel-integrated geometrical factors

 

 

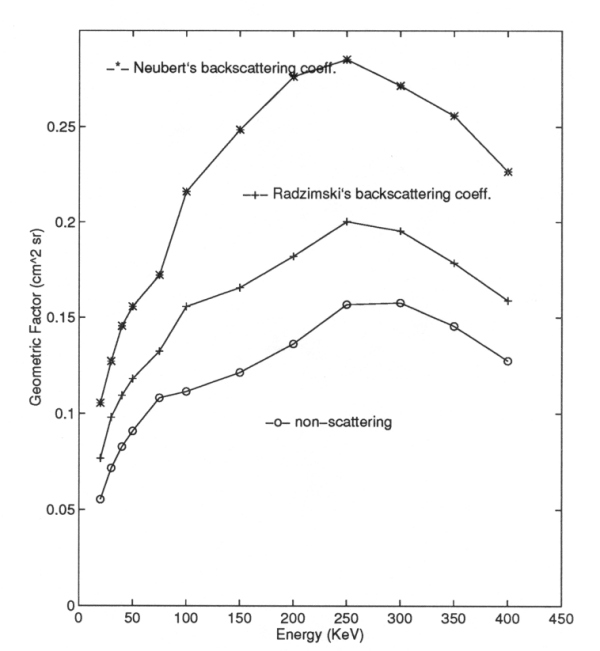
First, the backscattering coefficients are still uncertain, especially for oblique incidence in the energy range above 100 keV. Neubert's formula is obtained from the experimental data. But the data only includes energy ranges of 10-60 keV. Although the formula represents well those experimental data for oblique incidence, the extension of the formula to higher energies lacks experimental data for verification.

The backscattering coefficients given by Radzimski and Neubert include both elastic and inelastic backscattering, and we have used them here as if there was only elastic backscattering. The inelastic portion is small and we have not attempted to include this effect. The backscattering electrons go through a more complicated process than the elastic specular model used in this calculation. For more precise simulation we need to consider more realistic backscattering angular distributions.

 

The representation of the telescope aperture needs to be more precise. A more detailed simulation of the chamber of the telescope is needed as it would affect the direction of the backscattered electrons.

 

Nevertheless, the simplified backscattering model still gives some meaningful results for the DE1 and DE2 energy passbands when Radzimski's backscattering coefficients are used. Neubert's coefficients also yield good results for the DE1 channel. For other cases we may overestimate the geometric factors due to some of the reasons discussed above.

 

Figure A10-9 The geometric factor including specular backscattering (both Radzimski's and Neubert's backscattering coefficients) and non-scattering.

 

 

 

Next: A10.5 Appendix - Backscattering Coefficients