Ulysses HISCALE Data Analysis Handbook
Appendix 10. Effect of Backscattered Electrons on the Geometric Factors of the LEMS30 Telescope (Hong MS Thesis)
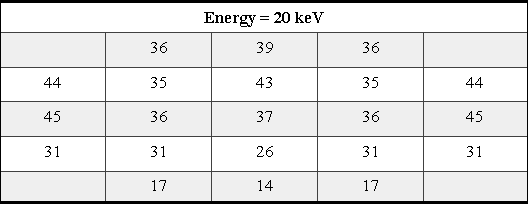
The following tables show the number of escapes for each area ΔAi and different energies. Each escape is an electron which starts from the center of the area ΔAi, makes its way out of the chamber of the telescope and reaches the aperture. The electron might not have any impact with the wall of the telescope, but if the electron hits the wall we assume the electron has a single elastic specular backscattering with the wall and continues its trajectory until it hits the wall (terminated) or the aperture (escape). The probability of the backscattering is determined by the energy, atomic number of the target and the incident angle of the electron. The probability formula is based on Radzimski's formula (see also section A10.7). For each area ΔAi an electron runs every δθ = 2º and δΦ = 5º and exhausts all possible polar θ and azimuth Φ angles.
Table A10-3 Escaping trajectories (Radzimski model)
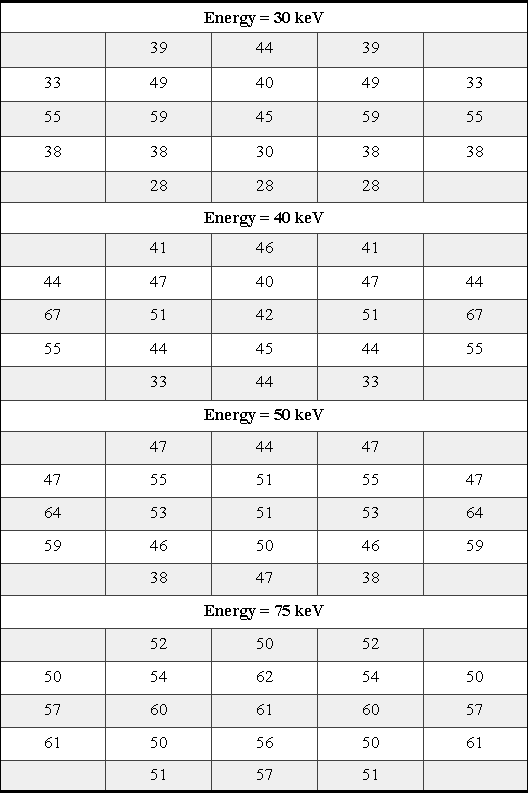

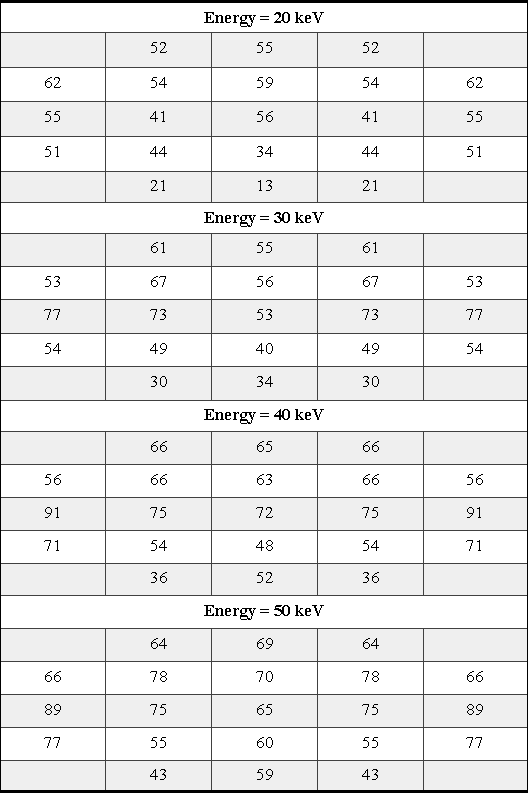
Given here are the results of the different backscattering coefficients which are based on G. Neubert and S. Rogaschewski's paper (Neubert, G., and Rogaschewski, S., Phys. Stat. Sol. (a), 59, 35, 1980). Other parameters are the same as the previous. The number of escapes without considering the backscattered effect is given later.
Table A10-4 Escaping trajectories, Neubert model


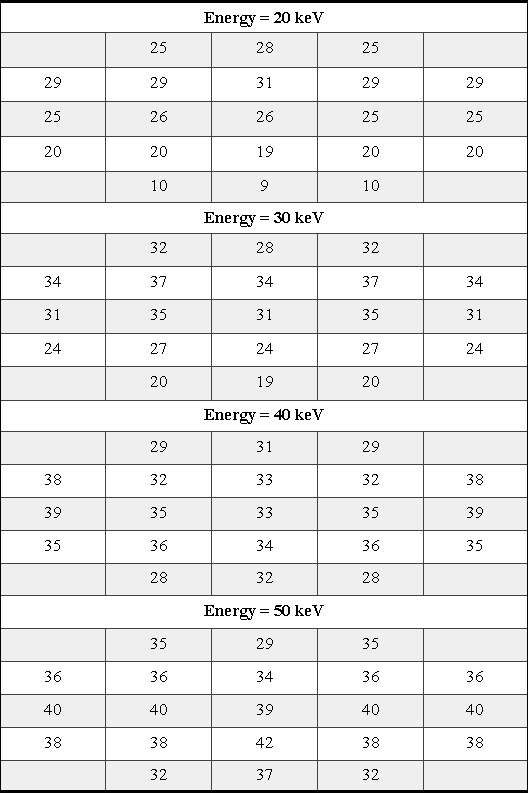
The following table shows the number of escapes for each corresponding area of DAi and different energies. Each escape is an electron which starts from the center of the area DAi and reaches the aperture of the telescope without any impact with the wall of the telescope. Those electrons that hit the wall would be terminated in their trajectory. Other parameters are the same as for the backscattering cases. For both cases the results are the same.
Table A10-5 Escapes without scattering


Next: A10.10 Appendix - Trajectories of the Escaped Electrons
Return to the Table of Contents for Hong's MS Thesis
Return to HISCALE List of Appendices
Return to Ulysses HISCALE Data Analysis Handbook Table of Contents
Updated 8/8/19, Cameron Crane
QUICK FACTS
Mission End Date: June 30, 2009
Destination: The inner heliosphere of the sun away from the ecliptic plane
Orbit: Elliptical orbit transversing the polar regions of the sun outside of the ecliptic plane



